Explanation of Lunar Eclipse Figures

Five Millennium Canon of Lunar Eclipses [Espenak and Meeus]

Lunar Eclipse Map Diagram

Earth will experience 12,064 eclipses of the Moon during the 5000-year period from -1999 to +3000 (2000 BCE to 3000 CE[1] ). An individual diagram and visibility map for every lunar eclipse over the five-millennium interval is presented on this Web site. The Moon's path through Earth's penumbral and umbral shadows illustrates the eclipse geometry, and the accompanying equidistant cylindrical projection[2] map shows the geographic region of visibility during every phase of each eclipse.

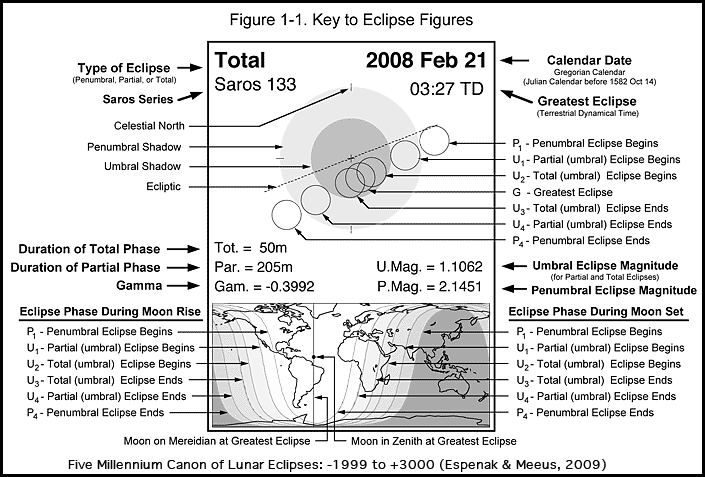
The figure for each eclipse consists of two diagrams. The top one depicts the Moon's path through Earth's penumbral and umbral shadows with Celestial North directed up. The Moon's orbital motion is from west to east (right to left)[3] with respect to the shadows. Each phase of the eclipse is defined by the instant when the Moon's limb is externally or internally tangent to the penumbra or umbra as follows.

Penumbral lunar eclipses have two primary contacts. Neither of these events is observable.

Partial lunar eclipses have two additional contacts as the Moon's limb enters and exits the umbral shadow (U1 and U4, respectively). At these two instants, the partial phase of the eclipse begins and ends.

Total lunar eclipses have two additional umbral contacts at the instants when the Moon's entire disk is first and last internally tangent to the umbra (U2 and U3, respectively). These are the times when the total phase of the eclipse begins and ends.

The instant when the Moon passes closest to the shadow axis is known as the instant of greatest eclipse. This corresponds to the maximum phase of the eclipse, and the Moon's position at this instant is also shown in the eclipse path diagrams.

The bottom diagram in each figure is an equidistant cylindrical projection map of Earth showing the geographic region of visibility at each phase of the eclipse. This is accomplished using a series of curves showing where Moonrise and Moonset occur at each eclipse contact. The map is also shaded to indicate eclipse visibility. The entire eclipse is visible from the zone with no shading. Conversely, none of the eclipse can be seen from the zone with the darkest shading.

At the instant of greatest eclipse, the Moon is deepest in Earth's shadow. A vertical line running through the middle of the clear zone (complete eclipse visibility) of a map indicates the meridian, or line of longitude, that the Moon is then crossing. An observer positioned somewhere on this line would then see the Moon at its highest point in the sky either due south or due north, depending on the observer's latitude and the Moon's declination. The geographic location where the Moon appears in the zenith at greatest eclipse is shown by a black dot on the meridian of greatest eclipse. All salient features of the eclipse figures are identified in Figure 1-1, which serves as the key to the figures on this Web site.

Data relevant to a lunar eclipse appear in the corners of each figure. To the top left, are the eclipse type (penumbral, partial, or total) and the Saros series of the eclipse. To the top right are the Gregorian calendar date (Julian calendar dates are used prior to 1582 Oct 14) and the time of greatest eclipse (Terrestrial Dynamical Time). The lower left corner lists the duration of the major phases of the eclipse in minutes. Depending on the eclipse type, the duration of the penumbral (P4 - P1), partial (U4 - U1), or total (U3 - U2) phases are given. Beneath the eclipse durations is the quantity gamma - the minimum distance of the Moon's center from the axis of Earth's penumbral and umbral shadow cones (in Earth equatorial radii) at the instant of greatest eclipse. The umbral and penumbral eclipse magnitudes[4] are given to the lower right.

A detailed explanation of the data in the lunar eclipse figures appears in the following sections.

Lunar Eclipse Type

There are three basic types of lunar eclipses:

  1. Penumbral - Moon traverses through Earth's penumbral shadow (Moon is partly or completely within the penumbra)

  2. Partial - Part of the Moon traverses through Earth's umbral shadow (Moon is partly within the umbra)

  3. Total - Entire Moon traverses through Earth's umbral shadow (Moon is completely within the umbra)

It is also possible for a penumbral eclipse to occur in which the Moon's entire disk is enveloped within the penumbra. Such events are called total penumbral eclipses. They are indicated by "(T)" after the penumbral eclipse type [i.e., Penumbral (T)].

With regard to total (umbral) lunar eclipses, most are non-central in that the Moon's disk misses the central axis of the umbral shadow cone. If a total eclipse is central, it is indicated by a "+" or "-" after the eclipse type, depending on whether the Moon's center passes north or south of the shadow axis (e.g., Total +).

Saros Series Number

Each lunar eclipse belongs to a Saros series using a numbering system first introduced by van den Bergh (1955). This system has been expanded to include negative values from the past, as well as additional series in the future. The eclipses with an odd Saros number take place at the descending node of the Moon's orbit, while those with an even Saros number take place at the ascending node.

The Saros is a period of 223 synodic months (˜18 years, 11 days, and 8 hours). Eclipses separated by this interval belong to the same Saros series and share similar geometry and characteristics.

Calendar Date

All eclipse dates from 1582 Oct 15 onwards use the modern Gregorian calendar currently found throughout most of the world. The older Julian calendar is used for eclipse dates prior to 1582 Oct 04. Because of the Gregorian Calendar Reform, the day following 1582 Oct 04 (Julian calendar) is 1582 Oct 15 (Gregorian calendar).

Pope Gregory XIII decreed the use of the Gregorian calendar in 1582 in order to correct a problem in a drift of the seasons. It adopts the convention of a year containing 365 days. Every fourth year is a leap year of 366 days if it is divisible by 4 (e.g., 2004, 2008, etc.). However, whole century years (e.g., 1700, 1800, 1900) are excluded from the leap year rule unless they are also divisible by 400 (e.g., 2000). This dating scheme was designed to keep the vernal equinox on, or within a day of, March 21.

Prior to the Gregorian Calendar Reform of 1582, the Julian calendar was in wide use. It was less complicated than the Gregorian calendar in that all years divisible by 4 were counted as 366-day leap years, but this simplicity came at a cost. After more than 16 centuries of use, the Julian calendar date of the vernal equinox had drifted 11 days from March 21. It was this failure in the Julian calendar that prompted the Gregorian Calendar Reform. For more information on this topic, see Calendar Dates.

The Julian calendar does not include the year 0, so the year 1 BCE is followed by the year 1 CE. (See: BCE/CE Dating Conventions) This is awkward for arithmetic dating calculations. In this publication, dates are counted using the astronomical numbering system, which recognizes the year 0. Historians should note the numerical difference of one year between astronomical dates and BCE dates. Thus, the astronomical year 0 corresponds to 1 BCE, and the astronomical year -100 corresponds to 101 BCE, etc.

There are a number of ways to write the calendar date through variations in the order of day, month, and year. The International Organization for Standardization's (ISO) 8601 advises a numeric date representation, which organizes the elements from the largest to the smallest. The exact format is YYYY-MM-DD where YYYY is the calendar year, MM is the month of the year between 01 (January) and 12 (December), and DD is the day of the month between 01 and 31. For example, the 27th day of April in the year 1943 would then be expressed as 1943-04-27. This Web site supports the ISO convention, but has replaced the month number with the three-letter English abbreviation of the month name for additional clarity. From the previous example, the date is expressed as 1943 Apr 27.

Greatest Eclipse

The instant of greatest eclipse occurs when the distance between the center of the Moon and the axis or Earth's umbral shadow cone reaches a minimum. Because of Earth's flattening, the instant of greatest eclipse differs slightly from the instant of greatest magnitude. In practice, Earth's atmosphere diffuses the edges of the penumbral and umbral shadows such that the difference between greatest eclipse and greatest magnitude cannot be distinguished observationally.

Lunar eclipses occur when the Moon is near one of the nodes of its orbit and, therefore, moving at an angle of about 5° to the ecliptic. Hence, unless the eclipse is perfectly central, the instant of greatest eclipse does not coincide with that of apparent ecliptic conjunction with Earth's shadow (i.e., Full Moon), nor with the time of conjunction in Right Ascension.

Greatest eclipse is given in Terrestrial Dynamical Time or TD, which is a time system based on International Atomic Time. As such, TD is the atomic time equivalent to its predecessor Ephemeris Time and is used in the theories of motion for bodies in the solar system. To determine the geographic visibility of an eclipse, TD is converted to Universal Time using the parameter ΔT.

A series of polynomial expressions have been derived to simplify the evaluation of ΔT for any time from -1999 to +3000. The uncertainty in ΔT over this period can be estimated from scatter in the measurements.

Duration of Eclipse Phases

The duration of a penumbral eclipse "Pen." is the time between first and last external tangencies of the Moon with the penumbral shadow (i.e., P4 - P1). Similarly, the duration of a partial eclipse "Par." is the time between first and last external tangencies of the Moon with the umbral shadow (i.e., U4 - U1). Finally, the duration of a total eclipse "Tot." is the time between first and last internal tangencies of the Moon with the umbral shadow (i.e., U3 - U2).

The duration given for each eclipse phase is rounded to the nearest minute.

Gamma

The quantity gamma is the minimum distance from the center of the Moon to the axis of Earth's umbral shadow cone, in units of Earth's equatorial radius. This distance is positive or negative, depending on whether the Moon passes north or south of the shadow cone axis.

The change in the value of gamma after one Saros period is larger when Earth is near aphelion (June-July) than when it is near perihelion (December-January). Table 1-1 illustrates this point using eclipses from Saros series 129 (near aphelion- table on left) and Saros series 134 (near perihelion-table on right).

Table 1-1. Variation in Gamma at Aphelion (on left) vs. Perihelion (on right)
Date Gamma Δ Gamma Date Gamma Δ Gamma
1928 Jun 03 -0.3175- 1928 Nov 27 0.3952-
1946 Jun 14 -0.2324 0.0851 1946 Dec 08 0.3864 -0.0088
1964 Jun 25 -0.1461 0.0863 1964 Dec 19 0.3801 -0.0063
1982 Jul 06 -0.0579 0.0882 1982 Dec 30 0.3758 -0.0043
2000 Jul 16 0.0302 0.0881 2001 Jan 09 0.3720 -0.0038
2018 Jul 27 0.1168 0.0866 2019 Jan 21 0.3684 -0.0036
2036 Aug 07 0.2004 0.0836 2037 Jan 31 0.3619 -0.0065
2054 Aug 18 0.2806 0.0802 2055 Feb 11 0.3526 -0.0093

A similar situation exists in the case of solar eclipses. The explanation can be found in van den Bergh (1955).

Eclipse Magnitude

The eclipse magnitude is defined as the fraction of the Moon's diameter immersed in Earth's shadows. Because there are two shadows-penumbral and umbral-there are two corresponding eclipse magnitudes. The eclipse magnitudes appearing in the figures are given at the instant of greatest eclipse when the Moon passes closest to the axis of the two shadow cones.

The penumbral eclipse magnitude of penumbral eclipses in this Catalog of Lunar Eclipses (hereafter referred to as the Catalog) ranges from 0.0004 to 1.0858 (Sect. 3.5). For most penumbral eclipses, the penumbral magnitude is less than 1 meaning only a fraction of the Moon's disk enters the penumbra. When the penumbral magnitude is greater than or equal to 1.0, the Moon's entire disk is immersed in the penumbra and the event is termed a total penumbral eclipse. It should be noted that penumbral eclipses are subtle events. In fact, they cannot be detected visually - with or without optical aid - unless the eclipse magnitude is greater than ˜0.6. The umbral eclipse magnitude of a penumbral eclipse is always negative. It is a measure of the distance of the Moon's limb to the edge of the umbral shadow in units of the Moon's diameter.

During a partial lunar eclipse, some fraction of the Moon's disk enters the umbral shadow. The umbral magnitude for partial eclipses in the Catalog ranges from 0.0001 to 0.9998. The Moon also passes through the penumbra during a partial eclipse so the penumbral magnitude is usually greater than 1. In the case of a total lunar eclipse, the Moon's entire disk passes through Earth's umbral shadow. During totality, the Moon can take on a range of colors from bright orange, to deep red, dark brown, or even very dark grey. The only light reaching the Moon at this time is heavily filtered and attenuated by Earth's atmosphere. The umbral magnitude for total eclipses in the Catalog ranges from 1.0001 to 1.8821.

For more information, visit Visual Appearance of Lunar Eclipses.

The information above is based on material previously published in:

Five Millennium Canon of Lunar Eclipses: -1999 to +3000 (NASA TP-2009-214172)

Return to main index for:

Five Millennium Catalog of Lunar Eclipses

Footnotes

    [1] The terms BCE and CE are abbreviations for "Before the Common Era" and "Common Era," respectively. They are the secular equivalents to the BC and AD dating conventions. A major advantage of the BCE/CE convention is that both terms are suffixes, whereas BC and AD are used as a suffix and prefix, respectively.

    [2] The equidistant cylindrical projection (also known as the equirectangular projection) is a simple x-y Cartesian map projection where lines of latitude and longitude are represented by straight, equally spaced horizontal and vertical lines.

    [3] By convention, maps are plotted north up, west to the left, and east to the right. This orientation assumes the viewer is looking down on Earth. But if the viewer turns around and looks up at the sky, the directions are reversed with east to the left and west to the right.

    [4] The eclipse magnitude is defined as the fraction of the MoonÕs diameter immersed in either EarthÕs penumbral or umbral shadows. It is a unit less parameter given at the instant of greatest eclipse.

References

Espenak, F, and Meeus, J. Five Millennium Canon of Lunar Eclipses: -1999 to +3000 (2000 BCE to 3000 CE), NASA Tech. Pub. 2008-214172, NASA Goddard Space Flight Center, Greenbelt, Maryland (2009).

van den Bergh, "Eclipses in the Second Millennium B.C. -1600 to -1207," Tjeenk Willink, and Haarlem, Netherlands (1954).

2009 Jan 29