Lunar Limb Profile

Eclipse contact times, the magnitude and the duration of totality all ultimately depend on the angular diameters and relative velocities of the Moon and Sun. Unfortunately, these calculations are limited in accuracy by the departure of the Moon's limb from a perfectly circular figure. The Moon's surface exhibits a rather dramatic topography, which manifests itself as an irregular limb when seen in profile. Most eclipse calculations assume some mean lunar radius that averages high mountain peaks and low valleys along the Moon's rugged limb. Such an approximation is acceptable for many applications, but if higher accuracy is needed, the Moon's actual limb profile must be considered. Fortunately, an extensive body of knowledge exists on this subject in the form of Watts' limb charts [Watts, 1963]. These data are the product of a photographic survey of the marginal zone of the Moon and give limb profile heights with respect to an adopted smooth reference surface (or datum). Analyses of lunar occultations of stars by Van Flandern [1970] and Morrison [1979] have shown that the average cross-section of Watts' datum is slightly elliptical rather than circular. Furthermore, the implicit center of the datum (i.e. - the center of figure) is displaced from the Moon's center of mass. In a follow-up analysis of 66000 occultations, Morrison and Appleby [1981] have found that the radius of the datum appears to vary with libration. These variations produce systematic errors in Watts' original limb profile heights that attain 0.4 arc-seconds at some position angles. Thus, corrections to Watts' limb profile data are necessary to ensure that the reference datum is a sphere with its center at the center of mass.

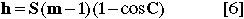
The Watts charts have been digitized by Her Majesty's Nautical Almanac Office in Herstmonceux, England, and transformed to grid-profile format at the U. S. Naval Observatory. In this computer readable form, the Watts limb charts lend themselves to the generation of limb profiles for any lunar libration. Ellipticity and libration corrections may be applied to refer the profile to the Moon's center of mass. Such a profile can then be used to correct eclipse predictions which have been generated using a mean lunar limb.

Along the 1997 eclipse path, the Moon's topocentric libration (physical + optical libration) in longitude ranges from l=+1.7° to l=+1.0°. Thus, a limb profile with the appropriate libration is required in any detailed analysis of contact times, central durations, etc.. Nevertheless, a profile with an intermediate libration is valuable for general planning purposes. The lunar limb profile presented in Figure 5 includes corrections for center of mass and ellipticity [Morrison and Appleby, 1981]. It is generated for 1:00 UT, which corresponds to the eastern Russia near the Mongolian border. The Moon's topocentric libration in longitude is l=+1.55°, and the topocentric semi-diameters of the Sun and Moon are 966.5 and 1005.8 arc-seconds, respectively. The Moon's angular velocity with respect to the Sun is 0.495 arc-seconds per second.

The radial scale of the limb profile in Figure 5 (at bottom) is greatly exaggerated so that the true limb's departure from the mean lunar limb is readily apparent. The mean limb with respect to the center of figure of Watts' original data is shown (dashed) along with the mean limb with respect to the center of mass (solid). Note that all the predictions presented in this publication are calculated with respect to the latter limb unless otherwise noted. Position angles of various lunar features can be read using the protractor in the center of the diagram. The position angles of all four contact points are clearly marked along with the north pole of the Moon's axis of rotation and the observer's zenith at mid-totality. The dashed line arrows identify the points on the limb which define the northern and southern limits of the path. To the upper left of the profile are the Sun's topocentric coordinates at maximum eclipse. They include the right ascension R.A., declination Dec., semi-diameter S.D. and horizontal parallax H.P.. The corresponding topocentric coordinates for the Moon are to the upper right. Below and left of the profile are the geographic coordinates of the center line at 1:00 UT while the times of the four eclipse contacts at that location appear to the lower right. Directly below the profile are the local circumstances at maximum eclipse. They include the Sun's altitude and azimuth, the path width, and central duration. The position angle of the path's northern/southern limit axis is PA(N.Limit) and the angular velocity of the Moon with respect to the Sun is A.Vel.(M:S). At the bottom left are a number of parameters used in the predictions, and the topocentric lunar librations appear at the lower right.

In investigations where accurate contact times are needed, the lunar limb profile can be used to correct the nominal or mean limb predictions. For any given position angle, there will be a high mountain (annular eclipses) or a low valley (total eclipses) in the vicinity that ultimately determines the true instant of contact. The difference, in time, between the Sun's position when tangent to the contact point on the mean limb and tangent to the highest mountain (annular) or lowest valley (total) at actual contact is the desired correction to the predicted contact time. On the exaggerated radial scale of Figure 5, the Sun's limb can be represented as an epicyclic curve that is tangent to the mean lunar limb at the point of contact and departs from the limb by h through the following equation.

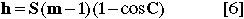
where: h = departure of Sun's limb from mean lunar limb

S = Sun's semi-diameter

m = eclipse magnitude

C = angle from the point of contact

Herald [1983] has taken advantage of this geometry to develop a graphical procedure for estimating correction times over a range of position angles. Briefly, a displacement curve of the Sun's limb is constructed on a transparent overlay by way of equation [6]. For a given position angle, the solar limb overlay is moved radially from the mean lunar limb contact point until it is tangent to the lowest lunar profile feature in the vicinity. The solar limb's distance d (arc-seconds) from the mean lunar limb is then converted to a time correction by:

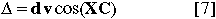
where: Delta = correction to contact time (seconds)

d = distance of Solar limb from Moon's mean limb (arc-sec)

v = angular velocity of the Moon with respect to the Sun (arc-sec/sec)

X = center line position angle of the contact

C = angle from the point of contact

This operation may be used for predicting the formation and location of Baily's beads. When calculations are performed over a large range of position angles, a contact time correction curve can then be constructed.

Since the limb profile data are available in digital form, an analytic solution to the problem is possible that is straightforward and quite robust. Curves of corrections to the times of second and third contact for most position angles have been computer generated and are plotted in Figure 5. In interpreting these curves, the circumference of the central protractor functions as the nominal or mean contact time (i.e. - calculated using the Moon's mean limb) as a function of position angle. The departure of the correction curve from the mean contact time can then be read directly from Figure 5 for any position angle by using the radial scale at bottom right (units in seconds of time). Time corrections external to the protractor (about half of all second contact corrections) are added to the mean contact time; time corrections internal to the protractor (all third contact corrections) are subtracted from the mean contact time.

Throughout Asia, the Moon's topocentric libration in longitude at maximum eclipse is within 0.3° of its value at 1:00 UT. Therefore, the limb profile and contact correction time curves in Figure 5 may be used in all but the most critical investigations.

Next section

Table of Contents